Merge Sort Algorithm

Merge Sorting algorithms are extremely important in computer science, used in everything from organizing data to improving (as much as possible) search sets of computer instructions. Among the different sorting ways of doing things, Merge Sort stands out due to its (wasting very little while working or producing something) and reliability. In this article, we will explore the Merge Sort set of computer instructions in depth, covering its ways of thinking/basic truths/rules, putting into use, and advantages. By the end, you will have a solid understanding of how Merge Sort works and how to put into use it in your projects.

What is Merge Sort?

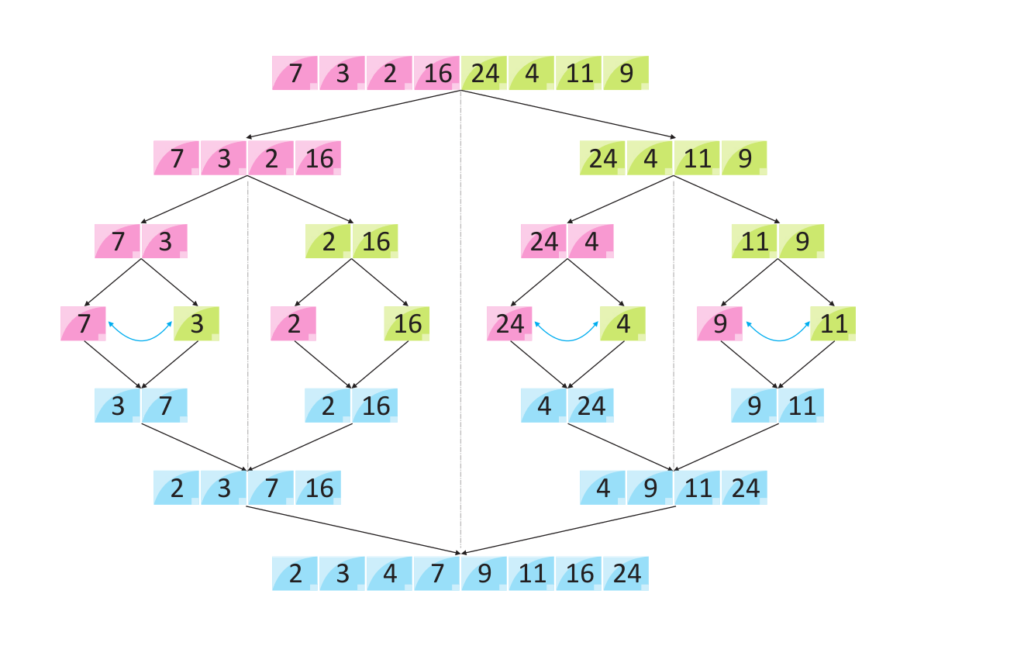
Merge Sorting is a comparison-based sorting set of computer instructions that follows the divide-and-win (by force) way of thinking. It was invented by John von Neumann in 1945. The basic idea behind Merge Sort is to divide the organized row into smaller sub-arrays, sort these sub-arrays, and then merge them back together into a single sorted organized row

Key Characteristics of Merge Sort:

1. Stable: Merge Sort maintains the relative order of equal elements.
2. Divide and Conquer: It divides the array into halves, conquers each half by sorting them, and then combines the sorted halves.
3. Recursive: The algorithm works recursively, continuously breaking down the problem into smaller sub-problems.
4. Time Complexity: O(n log n) for all cases (worst, average, and best).
5. Space Complexity: O(n) due to the use of additional arrays for merging.

How Merge Sort Works

Merge Sort works by splitting the array into smaller subarrays until each subarray contains a single element (which is inherently sorted). Then, it merges these subarrays back together in a sorted manner. Let’s break down the process:

1. Divide: Split the array into two halves.
2. Conquer: Recursively sort each half.
3. Combine: Merge the two sorted halves into a single sorted array.

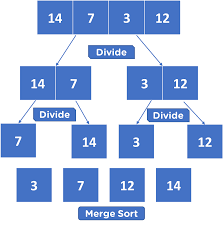
Detailed Steps

1. Splitting the Array:
   • Find the middle index of the array.
   • Split the array into two halves: left and right.
2. Recursive Sorting:
   • Recursively apply Merge Sort to the left half.
   • Recursively apply Merge Sort to the right half.
3. Merging the Sorted Halves:
   • Compare elements from both halves.
   • Place the smaller element into the new array.
   • Continue until all elements from both halves are merged.

Merge Sort Algorithm in Pseudocode

Here’s a high-level overview of the Merge Sort algorithm using pseudocode:

MergeSort(array)
  if length of array > 1
    mid = length of array / 2
    leftHalf = array[0:mid]
    rightHalf = array[mid:length of array]

    MergeSort(leftHalf)
    MergeSort(rightHalf)

    i = j = k = 0

    while i < length of leftHalf and j < length of rightHalf
      if leftHalf[i] < rightHalf[j]
        array[k] = leftHalf[i]
        i += 1
      else
        array[k] = rightHalf[j]
        j += 1
      k += 1

    while i < length of leftHalf
      array[k] = leftHalf[i]
      i += 1
      k += 1

    while j < length of rightHalf
      array[k] = rightHalf[j]
      j += 1
      k += 1

Implementing Merge Sort in Python

Let’s implement Merge Sort in Python. We’ll create a function to handle the sorting and a helper function for merging the arrays.

def merge_sort(array):
    if len(array) > 1:
        mid = len(array) // 2
        left_half = array[:mid]
        right_half = array[mid:]

        # Recursively sort each half
        merge_sort(left_half)
        merge_sort(right_half)

        i = j = k = 0

        # Merging the sorted halves
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                array[k] = left_half[i]
                i += 1
            else:
                array[k] = right_half[j]
                j += 1
            k += 1

        # Checking if any element was left
        while i < len(left_half):
            array[k] = left_half[i]
            i += 1
            k += 1

        while j < len(right_half):
            array[k] = right_half[j]
            j += 1
            k += 1

# Example usage
array = [38, 27, 43, 3, 9, 82, 10]
merge_sort(array)
print("Sorted array:", array)

   

Detailed Walkthrough of the Code

1. Base Case:
   • If the length of the array is greater than 1, proceed with splitting. Otherwise, the array is already sorted.
2. Splitting the Array:
   • Calculate the middle index and split the array into two halves: left_half and right_half.
3. Recursive Calls:
   • Recursively call merge_sort on left_half and right_half until the base case is reached.
4. Merging:
   • Initialize indices i, j, and k to 0. i and j are used to track positions in left_half and right_half, respectively, while k tracks the position in the original array.
   • Compare elements from left_half and right_half, and place the smaller element into the original array.
   • Continue until all elements from both halves are merged.
   • Copy any remaining elements from left_half and right_half into the original array.

Advantages of Merge Sort

1. Consistency:
   • Merge Sort has a consistent time complexity of O(n log n) for all cases, making it reliable for large datasets.
2. Stability:
   • It is a stable sort, meaning equal elements retain their relative order.
3. Parallelism:
   • The divide-and-conquer approach lends itself well to parallel execution, which can further optimize performance.

Disadvantages of Merge Sort

1. Space Complexity:
   • Merge Sort requires additional memory for the temporary arrays used during merging, resulting in a space complexity of O(n).
2. Complexity:
   • The implementation is more complex compared to simpler sorting algorithms like Bubble Sort or Insertion Sort.

Applications of Merge Sort

1. Large Data Sets:
   • Merge Sort is suitable for sorting large datasets due to its consistent time complexity.
2. External Sorting:
   • It is often used in external sorting algorithms where data is too large to fit into memory and needs to be sorted in chunks.
3. Linked Lists:
   • Merge Sort is preferred for sorting linked lists since it can efficiently handle the non-contiguous memory allocation.

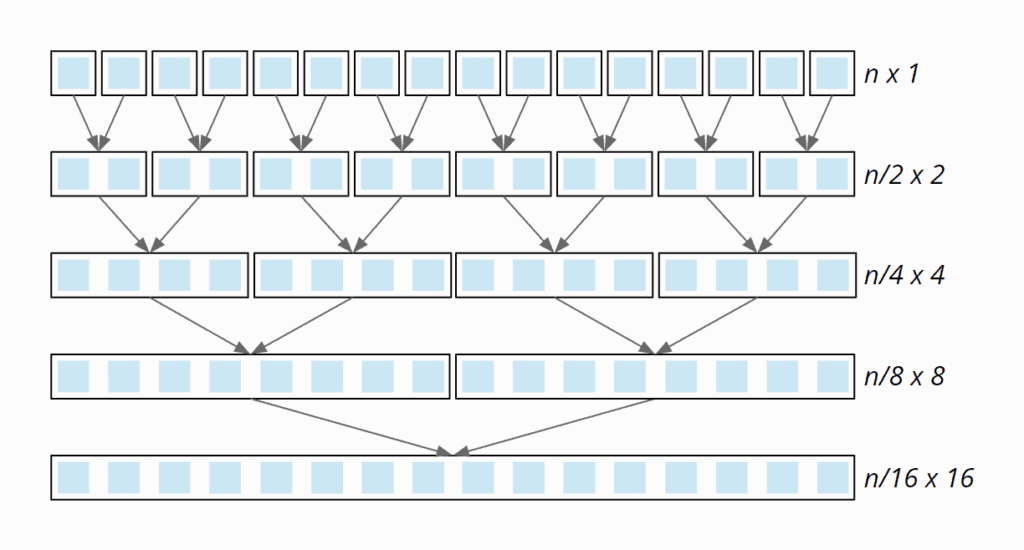
Optimizations and Variations

1. Bottom-Up Merge Sort:
   • A non-recursive version of Merge Sort that starts with small subarrays and iteratively merges them.
2. TimSort:
   • A hybrid sorting algorithm that combines Merge Sort and Insertion Sort. It is the default sorting algorithm in Python’s built-in sorted() function.

NOTE: You can also read C++ Arrays: Understanding and Implementing Arrays with Practical Examples

Conclusion

Merge Sort is a powerful and (producing a lot with very little waste) sorting set of computer instructions that excels with large datasets and stable sorting needed things. By breaking down the organized row into smaller sub-arrays and merging them back together, it (accomplishes or gains with effort) a time complex difficulty of O(n log n) across all cases. While it needs/demands added/more memory, the benefits of consistent performance and (firm and steady nature/lasting nature/strength) make it a go-to choice for many sorting tasks.

With a solid understanding of Merge Sort and its putting into use in Python, you can (in a way where you’re sure you are right) apply this set of computer instructions to your projects, securing/making sure of (producing a lot with very little waste) and reliable sorting of your data.

FAQS